Spaghetti and Hammers

Bloom filters were my first contact with probabilistic data structures a couple of years ago. Probabilitic data structures allow us to make a trade-off between the certainity of an operation and the space needed for the data structure. They are very useful for dealing with large amounts of data. They usually recur to one or more parameters to tune that certainity as we need.

Some of its more common applications include:

• Determining whether a user ID or domain is already taken
• Reducing disk lookups for the non-existing keys in a database
• Filtering out previously shown posts on recommendation engines
• Checking words for misspellings and profanity with a spellchecker
• Identifying malicious URLs, blocked IPs, and fraudulent transactions
• Counting the number of active users or total unique clicks on a website (with HyperLogLog, which is built on top of Bloom Filter)

What is exactly a Bloom filter?

As said before, a Bloom filter is a probabilistic data structure. It can be used to find if a given element is in the set with a certain error rate.

A Bloom filter provides only 2 operations: Adding an element and lookup an element. Removing elements is not supported in traditional implementations.

The lookup is the main operation. And there are two possible answers:

• The element is not present, which can be answered with full certainty;
• The element may be present in the set, where the certainty depends on the chosen parameters.

An important detail is that the more elements we add, the larger the probability of having false positives on the lookup.

How does a Bloom filter works?

A bloom filter relies in 3 parameters:

• a bitmap with m bits initiliazed as 0;
• k hash functions, which map a given element to one of the m bitmap positions;
• the number n of inserted elements.

It is important that each hash function is independent and uniformly distributed, otherwise the amount of false positives can get out of control. Speed of each hash function is also important for performance considerations.

Adding elements

To add a new element to the set we hash it with each of the hash functions. Each will return one bit to be set.

Let’s go through what happens when we try to add an element:

We’ll assume we have a Bloom filter where m = 10 and k = 3. As such we’ll have 3 independent hash functions and a bitmap with 10 elements (indexed from 0 to 9), each initialized as 0

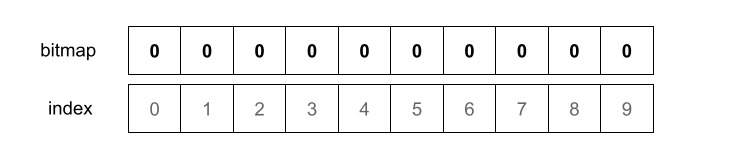
Now we want to add the element "random_string" to our Bloom filter. We start by hashing the element with the first hash function. The output of the hash function will determine what changes we’ll need to apply to the bitmap.

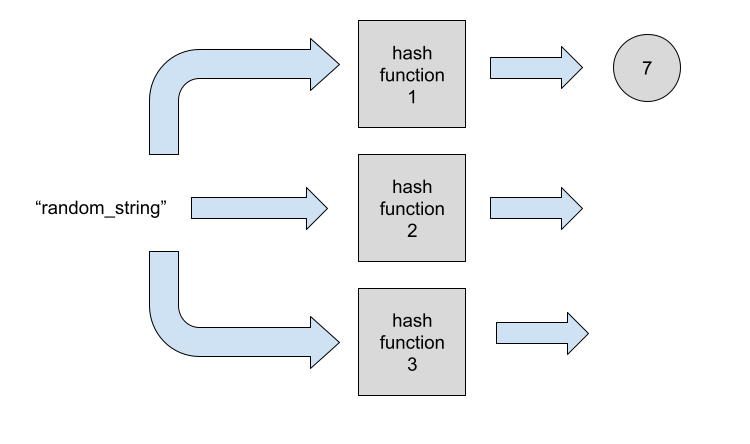
Let’ imagine the output is 7. This means we’ll mark the bitmap index 7 as 1.

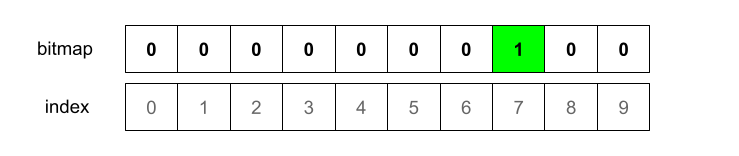
At this moment we have bitmap 0000000100. We now need to hash the element with the other two hash functions.

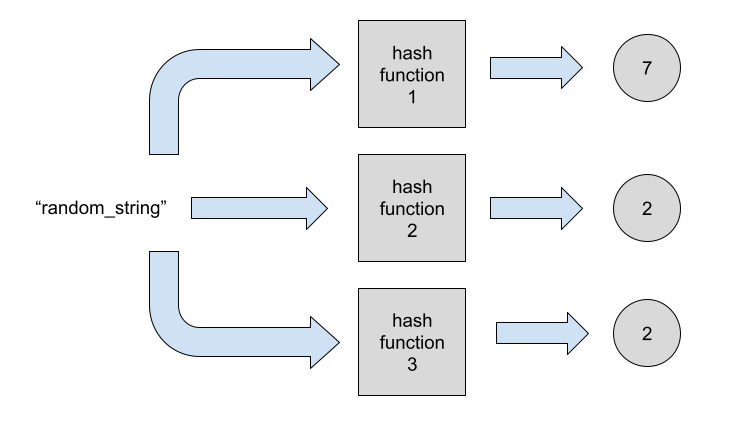
Notice that for this particular element the third hash function returned the same index as the second. For this reason we’ll have a no-op for the third hash function.

What if we added another element? Adding more elements would be just about repeating the process:

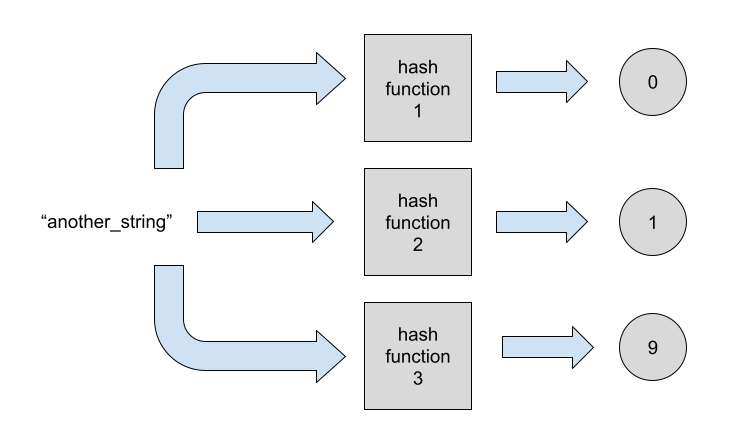
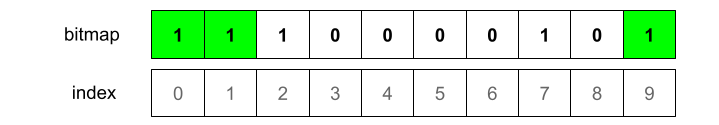
Lookup

How can we now check if some element exists in the Bloom filter?

Looking up for an element starts by hashing it through all the hash functions:

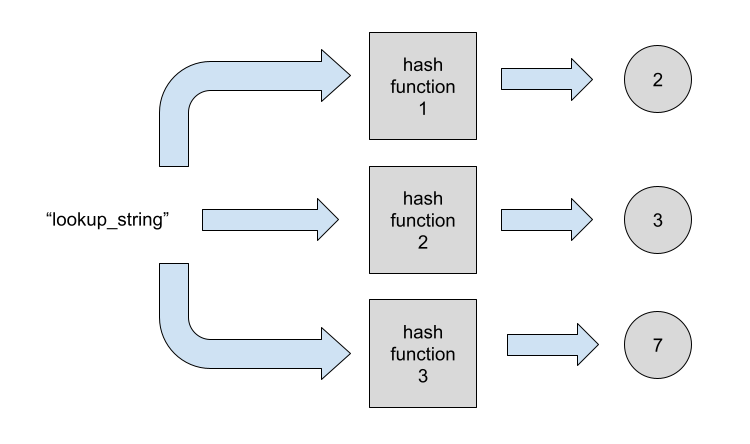
We now look if any of the indicated bits is not set. This would mean the element is not present for sure.

In this particular example, index 3 is not marked. So we know for sure the element was not added to the set before. Because if it had been added, those bits would be marked already.

On the other hand, if all bits are set, the element may be present. But it is also possible that those bits are set through an unfortunate combination of other elements. The likelihood of having that happening is controled by the m, k, and n parameters. And this is why the size of the bitmap and the number of hash functions is very important when using Bloom filters.

Which values should we choose for each parameter?

Classic answer: it depends. Mostly on the number of expected elements n.

We want to keep k a small number. The more hash functions we have, the slower will be our bloom filter. It will also fill up quicker since each hash function can fill another bit in the worst case. But if we have too few, we’ll have more false positives.

Wikipedia has a good section on the optimal number of hash functions, which I recommend you to read for more details, but the high level approach is the following:

1. We need to estimate the number of elements n we’ll have in our set;
2. We then need to choose a bitmap size, where we need to take into account our memory constraints;
3. We can compute the optimal value for k using the formula: (m/n)ln(2);
4. We finally compute the error rate using the formulas linked in the Wikipedia.
5. We can tune the error rate by trying other bitmap sizes in step 2.

There’s also this great website that computes all those parameters if we want to test them out.

Conclusion

Bloom filters are a widely used data structure when we have large amounts of data. Besides the classic implementation many other extensions exist (e.g. Counting Bloom filter).

Bloom filters are also just the entry point for many other probabilistic data structures.